Een van die moeiliker toepassings om mee te worstel, is die toepassing “Top-Hinged Flap”; Soms word (deur my) verwys as die “motorhuisdeurontwerp”. Vir verduidelikingsdoeleindes gebruik ons slegs terminologie wat in hierdie artikel uiteengesit is.
Voordat ons begin:
Daaris sakrekenaars daar buiteblik help met hierdie aansoek; Die meeste sal nie verklaar niehoe Hulle werk, hulle sal net 'n numeriese antwoord (of produkvoorstel) uitspoeg. Ten tyde van die plasing is ons 'top -skarnier' -sakrekenaar net 'n sigblad met vergelykings. Hierdie artikel handel meer oor die hoe. Ons hoop dat dit u help om verdere insig in u projek te kry.
Alhoewel hierdie toepassing intimiderend in die konsep lyk, kan dit opgedeel word in 'n vinnige trigonometrie en 'n hefboomgebaseerde berekening, wat albei maklik met 'n sakrekenaar of die internet gedoen kan word. Vir hierdie artikel gebruik ek die voorbeeld van 'n solder-aanhanger-dekking wat 'n klant voorheen gemaak het. Die waaier was in die muur, wat na buite lei, maar dit beteken ook dat hitte te maklik kon ontsnap gedurende die koue seisoene; Die eienaar wou dus 'n geïsoleerde dekking hê om hitte in die winter te help handhaaf, maar maak voorsiening vir maklike ventilasie in die somer (sonder om op die solder te klim om die flap te laat draai!).
Om te begin, het ons net diegewig van u skarnierflap (totale gewig) en dielengtevan die skarnier na die teenoorgestelde rand. Daar sal wiskunde voorlê.
Die gemerkte illustrasie hierbo toon die vereiste afmetings vir die toepassing (sonder werklike metings, in hierdie geval). Die belangrikste lengtes is die monteerpunt van die staaf op die klep, wat moet weesin die omtrek 20% -30% van die afstand van die skarnier tot by die rand van die bewegende deur.
Laat ons eers die monteerpunte definieer en verstaanhoekom Hulle moet net so wees; Die monteerpunt van die staaf sal ongeveer ¼ van die afstand van die skarnier tot by die rand wees, as die staafmonteringpunt te ver is, sal die krag wat van die aktuator benodig word, aansienlik styg, as dit te ver is, sal die aktuator -beroerte nie Pas korrek by die toepassing, wat lei tot 'n lift van minder as 90 grade. Hierdie punt is 'n benadering van die verhouding vir 'n gelukkige medium tussen die twee.
Deel een:Dwing dit
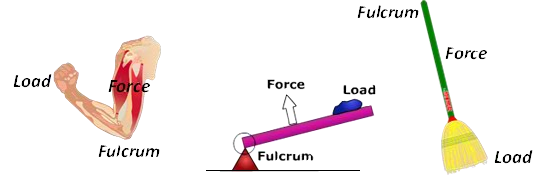
Die eerste berekening wat ons moet doen, is om diekrag op die aktuator. U kan hierdie toepassing herken as 'n klas 3 -hefboom (soos 'n vispaal of besem) - die las is aan die een kant, die skarnier is teenoorgesteld, en die moeite is tussen die twee.
Die vergelyking vir hierdie eenvoudige hefboomfunksie is:
-((Krag van aktuator) * afstand (aktuator -bevestigingspunt)) = ((Vrag van flap) * (lengte van die flap))
of
-(krag) = (las * lengte)/(monteerafstand)
ook uitgedruk met veranderlikes as:
-F = (l*d)/(m)
Nou, 'n paar getalle in die vergelyking inprop; vir hierdie voorbeeld kan sê die flap is 100 pond, en 30 "lank.
-F = (100# * 30 ") / (6")
-F = 3000/6
-F = 500 pond.
Soos u kan sien, hierdie tipe hefboomvereis 'n hoër vragaktuator. Dit doennie beteken dat u 'n 500 pond -aktuator benodig, dit beteken dat u 'nmeer as 500 pond aktuator Force.
Deel twee:Vind u spesifikasies
Eerstens om die nodige afstande uit te vind; hierdiesal wees Waar u verwag om u handboek vir trigonometrie van die hoërskool af te stof, maar u hoef nie. Ons sal dit gebruikenigste Om die ideale lengte van die aktuator -beroerte vir die toepassing te vind. Wat beteken dat ons net dieeen Vergelyking is diep in u onderbewussyn - die Pythagorese stelling.
A^2 +b^2 = c^2 waar a = flap montering posisie, b = die muurbevestigingsposisie, en c = u aktuator se verlengde lengte.
Hang aan, ons het neteen hiervan uitgepluis!
Korrek, nou is dit tyd virn bietjie Skat en kyk. Neem u tyd om ons webwerf te ondersoek, kyk na die spesifikasies en tegniese tekeninge van die aktueerders wat u dink kan werk - vir my voorbeeld, en as 'n algemene reël, sal ek die Premium aktuator lyn. As gevolg van die uitgebreide opsies vir die lengte van die beroerte en die gewigsgraderings tot 400 pond, is ditamper altyd Die beste 'gestandaardiseerde' beginpunt om te gebruik vir ramings.
Na bogenoemde instruksies; 'n 12 "premium aktuator het 'nverlengde lengte van ongeveer 28 ", wat dielangste moontlike beroerte sonder om ons deurklap te veel uit te brei, of die deur onder te bewerk. Ons sal prophierdie Uitgebreide aktuatorlengte in ons Pythagorese stelling as C.
A^2 +b^2 = c^2
waarA = 6 ", B = muurmontering posisie, enC = ~ 28.
(28^2) - (6^2) = b^2
784 - 36 = 748
sqrt (748) =27.349 ... = Geskatte muurmonteringsposisie (ongeveer 27.3 ')
Sit dit alles saam
Hieronder is die diagram wat u vroeër gesien het met 'n bietjie illustrasie; Dit wys dat die lengte van die aktuatorverander net effens Deur 'n 1-2 "offset op die basis van die eenheid (die muurmonterposisie) by te voeg
Met behulp van ons lengte -oplossing van Deel 2, weet ons dat die benaderde lengte van die aktuator wat ons oorweeg - die gewigsvereiste van Deel 1 egter hoër is as die aktuator waarvoor ons geskat is. Hoe kan ons dit oplos? Die maklikste opsie is om 2 aktuators te gebruik en die lasvereiste per aktuator in te verdeelhalf. Dit sal ons in staat stel om 2x 400 pond premium lynaktuators (insluitend optiese eenhede) te gebruik. As u aansoeknieSluit twee aktuators in, u moet 'n aktuator vind watoorskry Die gewigsvereiste van Deel 1, maar bly naby die lengte -vereiste vanaf deel 2. Vir hierdie voorbeeld sou 'n koeël .50 cal 8 "eenheid op 674 pond of hoër vir hierdie toepassing werk.
Dit was 'nKlompOm te oorweeg; Maar dit moet net een keer gedoen word; Noudat u u spesifikasies ken en 'n algemene idee het van watter aktuator u benodig, is u gereed om u te begin beplan FIRGELLI stelsel.
